
So, this is going to be equal to X to the negative twenty-fifth power. The negative 20 minus five cause we have this one right Well once again, we have the same base and we're taking a quotient. Negative twentieth power divided by X to the fifth power. And so, let's just do one more with variables for good measure. Of this right over here, you would make exponent positive and then you would getĮxactly what we were doing in those previous examples with products. 12 to the negative seven divided by 12 to the negative five, that's the same thing asġ2 to the negative seven times 12 to the fifth power.

Have to think about, why does this actually make sense? Well, you could actually rewrite this. You're subtracting the bottom exponent and so, this is going toīe equal to 12 to the, subtracting a negative is the same thing as adding the positive, twelve to the negative two power. So, this is going to be equal to 12 to the negative seven minus negative five power. So, what if I were to ask you, what is 12 to the negative seven divided by 12 to the negative five power? Well, when you're dividing, you subtract exponents if With one over A times A, which is the same thing asĪ to the negative two power. That cancels with that, and you're still left This right over here, that is one over A times A times A times A and then this is times A times A, so that cancels with that, Since I'm multiplying them, you can just add the exponents. What is that going to be? Well once again, you have the same base, in this case it's A, and so So let's say that you have A to the negative fourth power times A to the, let's say, A squared. So this four times four is the same thing as four squared.
Negative exponent rule reciprocal plus#
And so you're going to be left with five minus three, or negative three plus five fours. And so, three of these in the denominator are going to cancel out with three of these in the numerator. And so notice, when you multiply this out, you're going to have fiveįours in the numerator and three fours in the denominator. So it's times four times four times four times four times four. And then four to the fifth, that's five fours being Four to the negative 3 power, that is one over four to the third power, or you could view that as one over four times four times four. And that's just a straightįorward exponent property, but you can also think about why does that actually make sense. Four to the negative three plus five power which is equal to four See look, I'm multiplying two things that have the same base, so this is going to be that base, four. Well there's a couple of ways to do this. And I encourage you to pause the video and think about it on your own. So, let's think about whatįour to the negative three times four to the fifth power is going to be equal to. Therefore, the reciprocal of 8 1/11 is 11/89.- Let's get some practice with our exponent properties, especially when we have integer exponents. For example, the reciprocal of \(2\dfrac\) is the same as 89/11. The reciprocal of mixed fractions can be found by converting mixed numbers to improper fractions first, and then we can simply interchange numerator and denominator values. Now let us look at the reciprocal of mixed fractions and negative fractions in detail.
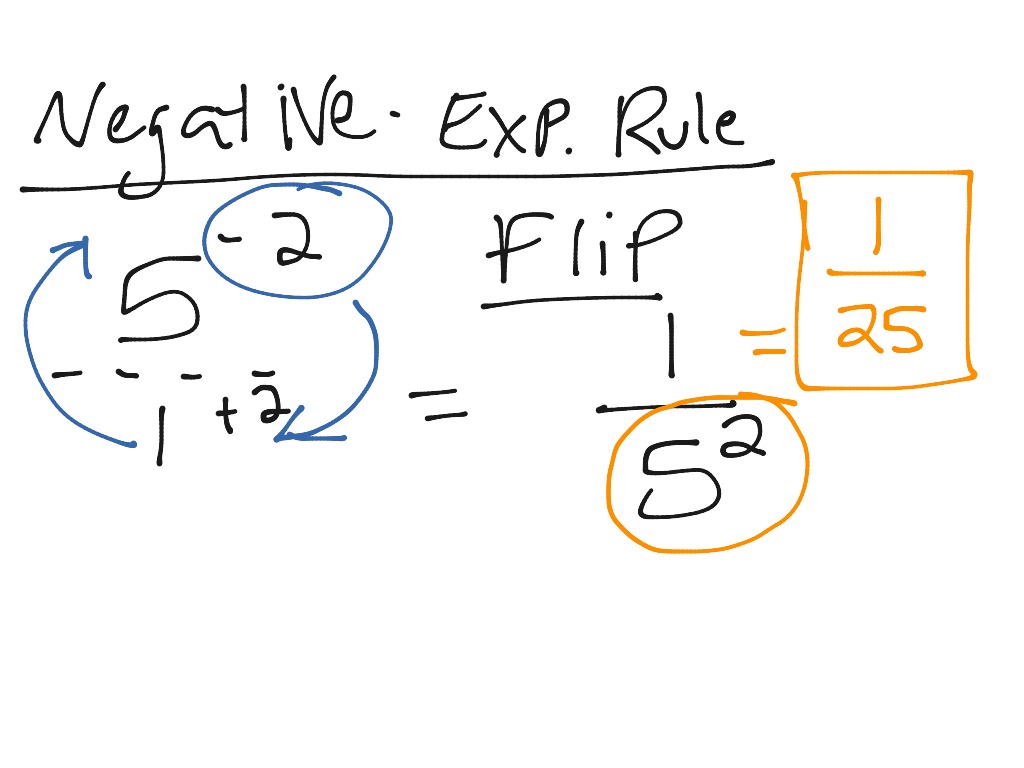
Negative exponent rule reciprocal free#
Use Cuemath's free online reciprocal calculator to verify your answers.


 0 kommentar(er)
0 kommentar(er)
